Does SARS-Cov2 mass testing make sense?
In four days from now, the first round of SARS-Cov2 mass testing is starting in Austria. Not really surprisingly, this topic has been dominating the political, scientific and colloquial debate of the recent weeks, even at my home. Well, let's have an objective look, how such an approach aiming at testing nearly the whole country's society with rapid antigen tests for SARS-Cov2 is going to work, if it can work at all and if it has a 'wave-breaker' potential in the current phase of coronavirus pandemic. And, important for all potential participants, we'll have a look what a positive or negative test result means to you.
Principle of diagnostic testing: true, false results and beyond
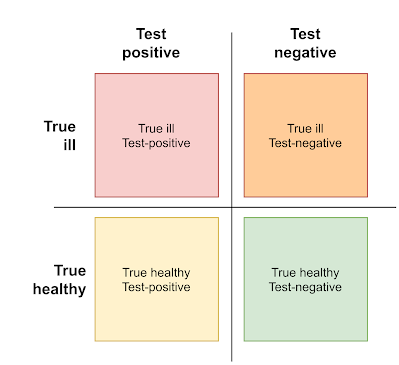
If you are a data or healthcare professional you may well skip this first few sentences or treat them as a small refresher (and please make sure you read it if you're a politician...). As almost every diagnostic procedure in real life, from the pregnancy test to the debugger of your favorite programming language, no test for SARS-Cov2 is ideal. This means, that it may indicate correctly the infection or fall positive if you are healthy for instance. There are four possible outcomes of the test, as presented in the Graphic 1 below:
- The first test outcome is the most desired one: the test detects truly ill or SARS-Cov2 infected individuals
- The second outcome is not so fine, especially for the tested person: the test is positive but there's no infection and you'll spend the next ten days at home and probably ask yourself why. You are then so called False Positive (FP). This has obviously no impact on the pandemic and as such is not so critical for the net effect of the mass testing
- The third outcome is a nightmare of the policy makers and health authorities: your test is negative but you are infected, so called False Negative (FN). You're probably convinced that even if having a cold, it's for sure not a SARS-Cov2 and, depending on your behavior, may spread it
- The fourth outcome makes all happy: you are healthy and test-negative
The math behind it is really simple and summarized in Graphic 2. To help us measure, how good a test is, two parameters are defined: sensitivity and specificity. The sensitivity is the fraction or percent of the infected individuals or True Positive (TP) which are detected by the test. The specificity does the same for the healthy subset: it's the fraction or percent of the uninfected population or True Negative (TN) receiving a negative test result.
Graphic 2. Math behind diagnostic test principle
For you as a mass test participant it's probably quite important how high the probability of being really coronavirus-infected really is, if your test is positive. This probability is termed Positive Predictive Value (PPV). Analogically, if your result is negative, you may want to know, how likely it is that you're really SARS-Cov2-free: this figure is termed Negative Predictive Value or NPV. Knowing the NPV, you'll easily calculate the likelihood of being infected with a negative result: simply subtract 1 - NPV.
You may have probably noted that sensitivity and specificity are the properties of the testing method or testing reagent. PPV and NPV, in turn, depend on the real prevalence of COVID-19 in the population given by the TP and TN figures. This means that even if a test is extremely specific and sensitive, probability that the test positive person is really infected may lay at few percent, if prevalence of COVID-19 in the population is low, let's say below one percent. In other words, the test will detect much more seemingly infected people that true SARS-Cov2 carriers.
In summary, knowing the sensitivity and specificity of the test, the size of the tested population and having a reliable estimate of the real infection prevalence, we can easily predict the results and efficacy of the mass testing campaign. Let's have a look!
Mass testing in Austria: will it work?
A week ago the mass testing campaign was held in the northern autonomous province of Italy, South Tyrol. The results of the action with almost 100% frequency turned out to be a surprise for everyone: roughly one percent of the population older than six was detected positive. Following the discussion on fora of the South Tyrolean media, most inhabitants and experts had expected something like three, five or even ten percent. Well, mass testing is a huge experiment: in particular, if you have no idea about the real prevalence before the mass test and the real-life goodness of your test reagents.
The situation in Austria is a bit different. There's a pretty decent estimate of SARS-Cov2 prevalence in the population measured by so colloquially called 'Dunkelzifferstudien' or dark figure test. A summary of results of the last of them, held on 12 - 14th November, was published last week (access on 2020-11-30). In short, the prevalence was estimated 3.1% (95% confidence interval/95%CI: 2.2%, 4.0%). Out of the individuals tested positive (72 out of 2263), one-third (24) were already tested positive by the authorities and in curfew. This means that 66% percent of the cases, mostly with mild cold symptoms and asymptomatic still run around, go shopping and to work. So, roughly 2% of the population not being in quarantine is currently carrying the pathogen. And they should be found by the mass test.
Before something about the results can be said, we need to know the sensitivity and specificity of the testing method. Cause there is no official information on the manufacturers and testing products (@policy makers: more transparency motivates to participate in the test!), we have to resort to product specs and published and pre-print (o tempora o mores!) studies. Roche, if one believes the gossips, one of the providers of the testing kits for the Austrian campaign, is proud of 96.52% sensitivity and 99.68% specificity. This figures were verified by Igloi and colleagues with the sensitivity of 94.3% and 99.5% specificity in a collective of high virus burden samples (Ct < 30). When low-virus samples were included, 84.7% sensitivity and 99.5% specificity was reported. Another test provider, Abbott, informs about 91.4% sensitivity and 99.8% specificity. Again, Linares et al, tried to corroborate those figures and obtained 73.3% and modest 54.5% sensitivity for the population of symptomatic COVID-19 ill and the mixed set of COVID-ill and their contact persons, respectively. The study doesn't report on specificity: I assume, it's similar to 99.8% as provided by the manufacturers.
In general, I have to underlie, that such rapid antigen tests are developed to test symptomatic cases and not the general population with some percent of low virus burden individuals without symptoms. There, the sensitivity is likely to be much lower and I regard the pessimistic value of 54.5% by Linares et al as the most probable one.
Modeling approach: it will work
As pointed above, having such data, it's not hard to model the expected results of the mass testing in Austria. To this end, I've created a tiny R project; as usual, you may play around with the scripts and result summary.
The modelling assumptions were:
- The estimated SARS-Cov2 prevalence in the 'quarantine-free' population based on the recent dark figure study of 2.1% (95%CI: 1.6%, 2.7%). The distribution, expected values and confidence intervals of the probable infection rates and the test results was obtained by bootstrapping of the dark figure study results
- Modeling was done with the six sensitivity/specificity scenarios described above (Abbott specifications, Abbott symptomatic by Linares, Abbott whole set by Linares, Roche specifications, Roche high virus by Igloi and Roche whole set by Igloi)
- The mass study population was a bit naively assumed 7,601,509 - it is the whole Austrian population older than 14
First let's have a look at expected percents of positive tests and compare them with the estimated SARS-Cov2 prevalence (Graphic 3).
Graphic 3. Expected positive results of the mass testing in Austria. True value: fraction and absolute number of infected inhabitants according to the dark figure study. Orange diamonds represent the expected values, whiskers span over 95% confidence interval (obtained by bootstrapping), points represent single bootstrapping iterations for the infection rate.
As expected, the fraction of positive test results depends both on the prevalence and sensitivity of the test kit: even with the most pessimistic test specifications by Linares, about 100,000 positive results are expected. Interestingly, for Roche, the rate of positive tests may exceed the real prevalence and numbers of positive results in the 150,000 to 200,000 range are expected. Pretty bad news, if you'd like to verify them with the gold standard PCR (Polymerase Chain Reaction) or perform systematic contact tracing.
The good information is that, thanks to excellent specificity, only a minority of these positive test results will be false positive (Graphic 4) and quite independently of the real SARS-Cov2 prevalence. Roughly, 2 - 5 promille of all test results will fall into this category, which means that 15,000 to over 35,000 individuals will unnecessarily stay at home - for the policy makers, in turn, just another argument against re-testing the positives with PCR.
Graphic 4. Expected false positive results of the mass testing in Austria. Orange diamonds represent the expected values,
whiskers span over 95% confidence interval (obtained by bootstrapping),
points represent single bootstrapping iterations for the infection rate.
Another good portion of news, this time for the authorities, is that the even assuming the lowest test sensitivity of 54% combined with the excellent specificity of over 99%, the false positives are not a considerable fraction of the positive test results. In other words, you'll be still able to isolate more than a half of the infected population.
On the other side, the fraction and number of false negatives may vary considerably with the scenario (Graphic 5). Obviously, the low sensitivity as proposed by Linares for a cohort including asymptomatic virus carriers will result in a false negative rate of roughly 1% or more than 70,000 individuals. In turn, if the test proves as sensitive as claimed by the manufacturers, less than 30,000 false negative results are expected. Whatever the scenario, if you're tested negative, probably it is not a brilliant idea to go skiing afterwards, visit your grandparents or celebrate Christmas with your friends.
Graphic 5. Expected false negative results of the mass testing in Austria. Orange diamonds represent the expected values,
whiskers span over 95% confidence interval (obtained by bootstrapping),
points represent single bootstrapping iterations for the infection rate.
Finally, let's delve into the predictive values. First of all, how likely it is, that your positive result means the Cov infection. As shown in Graphic 6A, it's very likely due to the perfect specificity of all tests: in more than 75% of cases the positive result will be correct and isolating you may help to brake the pandemic. This is obviously another argument for the policy makers not to re-test with PCR.
Graphic 6. Expected positive predictive value and probability of being infected despite negative result in the Austrian mass testing campaign. Orange diamonds represent the expected values,
whiskers span over 95% confidence interval (obtained by bootstrapping),
points represent single bootstrapping iterations for the infection rate.
When you ask, what are the chances that you're a virus carrier with a negative mass test result - please note, that the figure presented in Graphic 6B looks quite similar to the false negative results. If the sensitivity of the test falls low, like in the scenario by Linares, it may reach up to 1%. For comparison, your chances before the mass test are about 2%. As underlined before, still a lot and not really a reason to change your behavior and, from the sight of the authorities, to rapidly loosen the lockdown policies.
Collectively, mass testing from the purely statistical perspective may become a great tool to combat the SARS-Cov2 pandemic, even if the test sensitivity is low. I'll keep you up to date with the real sensitivity and specificity of the mass testing as soon as the results of the Austrian campaign are published!
Comparative approach: it will work or it won't
All models are bad, but some useful - this statement belongs for me to the central theorems of statistics... There are two regions of Europe, which have already held mass testings: Slovakia and the autonomous province of Italy, South Tyrol. As most regions of Europe, those two experience quite hard lockdown of social life and the mass testing was praised as a way from the crisis. Let's investigate, if it was.
The Slovakian mass test was finalized on 1st November at the peak of the local second wave of the pandemic. At the first look on a plot of daily new cases for 100,000 inhabitants of the country, one can not state that the mass testing proved a 'wave breaker' (Graphic 7A): the weekly trend of infections could not be substantially altered. This observation is confirmed by a statistical comparison of the daily incidence two weeks before the test and two weeks after
(Graphic 7B; I know, T test is not the proper tool there, an anomaly analysis will come in an update of the post). In simple words, the testing in Slovakia did not work.
(Graphic 7B; I know, T test is not the proper tool there, an anomaly analysis will come in an update of the post). In simple words, the testing in Slovakia did not work.
Graphic 7. (A) Effect of mass testing on daily new cases of Cov-19 in Slovakia and South Tyrol: the date of the campaign is represented by thick solid line. The data for the Italian province Trentino, where no mass testing took place are presented for comparison; dashed line represents the date of the South Tyrolean mass testing. (B) Daily new cases in Slovakia, South Tyrol and Trentino 14 days before and 14 days after the campaign compared by two-tailed T test. Note, for Trentino, the date of the South Tyrolean test was taken as a reference. Source of daily case data: ECDC and Wikipedia.
The situation for South Tyrol is fairly different. Still it's over a week post testing and too early to observe any long-term consequences. Nevertheless, we can compare the daily incidence with the neighbor Italian province Trentino with an almost identical population, analogous testing strategies and lockdown policies. As shown in Graphic 7A and B, the daily cases in South Tyrol seem to fall, which is not the case for Trentino - the incidence before and after the test is significantly lower in the first province but not in the later one. Cautiously stated: it seems to have functioned in South Tyrol.
The big question is why. In both Slovakia and South Tyrol the percent of the tested target population (over 10 and over six years old, respectively) was close to 100% - so missing large groups of the society was not the case. To me, the most conspicuous difference was the size of the tested population and logistics: South Tyrol is 10 times smaller than the East European country, which presumably enabled better coordination of the testing procedure, digitization of result processing and delivery and keeping hygiene standards more tight. At the end of the day, it should be avoided that you catch the virus waiting with hundred other citizens at the testing point for your result.
As stated before, none of the regions tried to perform even a basic contact management of the cases identified positive by mass testing. In practice, a positively tested citizen was locked at home but their co-habiting relatives and friends or work colleagues were not, provided a negative test result. We need to keep in mind that the test positivity or negativity reflects just the particular moment of testing. You may already have the pathogen in your body but at a such low burden that it was under the detection limit of the test. But tomorrow or a week later, you may develop full-blown symptoms! For Slovakia this may already explain the failure, for South Tyrol this means, that the success at reducing daily incidence may turn out to be very transient - I'll keep you up to date!
Summary: is it worthwhile?
To sum up, what we found already:
- Mass testing can reduce the prevalence of SARS-Cov2 in the population and daily incidence. Whether it's a 80%, 50% or 30% reduction depends on the sensitivity of the test. Notably, the real-life sensitivity in a huge cohort with few percent asymptomatic individuals or those with mild symptoms is a great unknown
- All rapid antigen tests show an almost perfect specificity, so the number of false positive results of the mass testing is negligible. Re-testing the positive cases with PCR will only strain the testing resources needed for traditional containment management
- The figure of false negatives depends on the test sensitivity and may be considerably high. For this reason, mass testing can not replace 'traditional' containment measures such as social distance, hand hygiene, contact reduction or face mask
- For the participant: the likelihood that your positive test means a SARS-Cov2 infection is between 75% to 90%, so the risk of being false positive is with the current disease prevalence is low. However, depending on the sensitivity, the probability of being infected despite the negative result may be as high as 1% - not much less than before the mass testing. This means, the negative result should not be misunderstood as a permission for intensified social contacts
With this in mind, it's fully legitimate to ask, if the cost of the campaign does not surpass the advantages and if other containment management strategies or testing and protection of the risk groups won't turn out more effective. Investigating that with hard data is certainly an attractive topic for some future post!








Comments
Post a Comment